2進数で引き算をしよう
例題
H22.春 問3
負数を2の補数で表すとき、すべてのビットが1であるnビットの2進数“1111…11”が表す数値又はその数式はどれか。
ア -(2n-1-1) イ -1 ウ 0 エ 2n-1
手順
説明が長くなったので手順を先に示します。その後でちゃんと解説します。
1. 桁数(ビット)を決める
1111...11のままではわかりづらいので、ここでは4けたの数値1111とします。
2. 符号と数値で分ける
「負数を2の補数で表すとき」という表現があるので、1111の先頭ビットは符号です。
1と111に分けて考えます。
3. (符号がマイナスのときは)絶対値をひっくり返して+1する
0が+、1が-なのでこの111は負数(マイナス)です。マイナスなのでひっくり返すと、000です。さらに1を足します。
000 + 001 = 001
4. 符号をくっつける
最後に符号を付けると -001,つまり-1 になりました。よって、答えはイです。
解説
考え方
手順を見てのとおりなかなかめんどくさそうです。そもそもなんでこんなことをするのかっていうと、「足し算だけで引き算がしたいから」です。これが理解出来れば2進数の引き算は大丈夫です。大事なのでもう一度言います。なぜ2の補数だなんやかんやと面倒なことをするのかというと、
「足し算だけで引き算がしたいから」
です。
1. 桁数(ビット)を決める
僕みたいな数学アレルギー持ちは「nビットの2進数」とか言われるとなんだか、公式があってそれを覚えてなきゃいけないのかと思ってしまいます。
確かに問題の条件下では11も1111も、11111111も同じで、答えは-1なんだけど、これは暗記とかそういう話じゃありません。
ここでは具体的な数値、4ビットの1111をしっかり見ていきましょう。
2. 符号と数値で分ける
前回までの知識では、2進数で表現できない数値があります。それが負数、つまりマイナスの値です。
図のように、先頭ビットの0と1でプラス、マイナスを表現するのです。
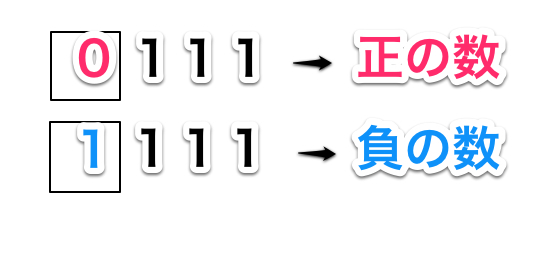
先頭が符号、残りが数値、という具合に分けることができました。
3. ひっくり返して+1すりゃいい
先頭が符号、ということが分かったら今度は”2の補数”という考え方が出てきます。結論から言うと、覚えることは一つだけです。この呪文さえあれば大丈夫です。
2の補数 = ひっくり返して+1した数
いろいろ説明を考えましたが、いっきに説明すると辛くなるのでここでは魔法をかけられた仮の姿として話を進めます。
1 マイナス 111 魔法をかけられた仮の姿
1111の1は符号、111は魔法をかけられた数。とにかく、111は絶対値とは違う仮の姿。図にするとこんな感じです。

問題に答えるにはこの仮の姿である111から魔法を解いてあげて、絶対値にすることが必要です。そこで出てくるのが先にあげた呪文です。
2の補数 = ひっくり返して+1した数
111をひっくり返して+1すると001となりますね。
ひとまずは、「111の2の補数は?」と聞かれて、
(ひっくり返して000、+1すると...)「1だ!」
と答えられればOKです。簡単ですね。流れを遮断するのが気持ち悪いので、とりあえずそういうもんだってことにしておきます。
4.符号をくっつける
絶対値がでてきたので後はマイナスの符号をつければ出来上がり。答えはめでたく-1になりました。
2の補数、魔法の中身は?
なんだか複雑だな、と感じたのは魔法の中身です。お気に入りのキタミ式の参考書を持ってしても理解するのに苦労しました。
ぶっちゃけこれは魔法でも何でも無く、左記に述べた通り「足し算で引き算をするため」にこうしているだけなのです。